​牟合方盖的创造及履历意思 估计体积的方式是什么?

牟合方盖的创造及履历意思 估计体积的方式是什么?

牟合方盖是什么？信赖许多人关于于这个都很生疏，牟合方盖是由我国盘古的数学家刘徽创造的一种用于估计球体体积的办法，他期望不妨用牟合方盖来证据《九章算术》的公式有过失，然而是末尾也不实行，然而是牟合方盖的创造有要害的履历意思，牟合方盖是怎么样估计球体的体积估计办法的？

牟合方盖是什么？

牟合方盖，由我国盘古数学家刘徽最先创造并采取的一种用于估计球体体积的办法，相似于当前的微元法。因为其采取的模子像一个牟合的方形盒子，故称为牟合方盖。

牟合方盖指的是什么？

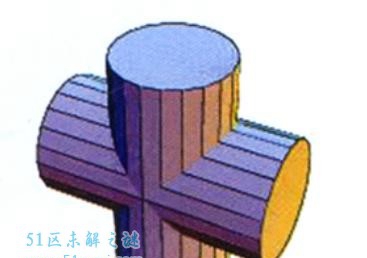
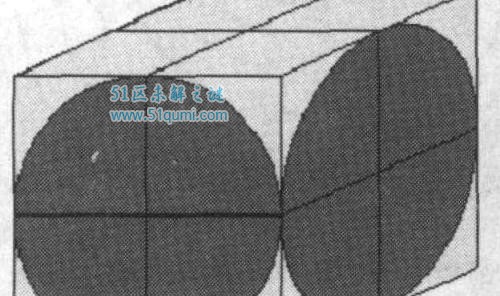
牟合方盖便是当一个正立方体用圆规从纵横二侧面作内切圆柱体时，二圆柱体的大众局部。刘徽在他的注中关于“牟合方盖”有以下的刻画：“取立方棋八枚，皆令立方一寸，积之为立方二寸。规之为圆囷，径二寸，高二寸。又复横规之，则其形有似牟合方盖矣。八棋皆似阳马，圆然也。按合盖者，方率也。丸个中，即圆率也。”本来刘徽也是期望经过构作一个立体图形，它的每一个横切面皆是正方形，并且会外交于球体在一致高度的横切面的圆形，而这个图形便是牟合方盖，因为刘徽只了解一个圆及它的外交正方形的面积比为π：4，他期望不妨用牟合方盖来证据《九章算术》的公式有过失。

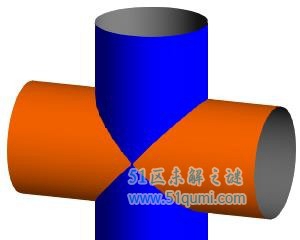
天然他也期望由这方面动手求球体体积的精确公式，因为他了解牟合方盖的体积跟内交球体体积的比为4：3，只消有办法找出牟合方盖的体积便可，只痛惜，刘徽终究不行处理，他只不妨指出处理的办法是经过估计出外棋的体积，然而因为外棋的外形搀杂，所以不胜利，他无奈地只佳留待有能之士希图处理的办法：“瞅立方之内，合盖除外，虽衰杀有渐，而几不掩。判合归纳，周围相缠，浓纤诡互，不行等正。欲陋形措意，惧失公理。敢不阙疑，以俟能言者。”

牟合方盖的体积估计办法：

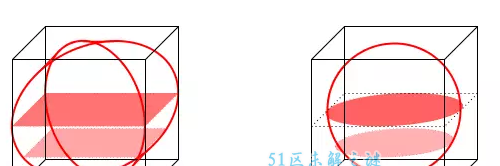
上头右图是一个正方体掘去了二个四棱锥（这二个四棱锥分离以左右底面为底面，以正方体的核心为极点），设正方体边长为2r。以平行于底面的平面共时截“牟合方盖”和“右图的几许体”，所得截面如上图所示。左图的截面是一个正方形，设核心到截面的隔绝为h，可得该正方形边长为2√r²-h²，所以左图的截面面积为4（r²-h²）

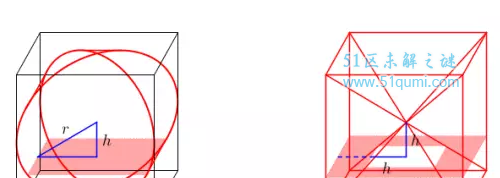
右图的截面像一个正方环形，面积是大正方形的面积减去小正方形的面积，边长为2r，所以大正方形面积为4r²，共样设核心到截面的隔绝为h，可知小正方形的边长为2h，所以小正方形的面积为4h²，即截面面积为4r²-4h²。

由上可知，二几许体在一致程度位子的截面面积十分，依据祖暅本理，它们的体积十分，右图的体积即是正方体的体积减去二个四棱锥的体积，依据锥的体积公式可知，二个锥的体积之和为正方体体积的1/3，所以该几许体的体积为正方体体积的2/3，即“牟合方盖”的体积为正方体体积的2/3，正方体体积为8r³，所以最后，“牟合方盖”的体积为16r³/3。

牟合方盖的履历意思：

“牟合方盖”的提出，充足表现了昔人丰厚的设想本领，以及为处理问题修树模子的聪明。刘徽是1700多年前的人，以千年前的社会常识程度，便在思索这种问题，几乎令人叹为瞅止，这种聪明的光线，震古烁今，灿烂世界。他们关于数学大概者哲常识题的执着思索与纯正摸索的精力，是新颖人身上及其缺少的，也是现行培养缺失的一个要害方面。