​共角定理是几年级学的 共角定理怎么证明

共角定理是几年级学的 共角定理怎么证明

标题：共角定理

作者：张景中□中国科学院院士

彭翕成□华中师范大学教育信息技术工程研究中心

共角比例定理

在三角形中，角与边总是相对的．那么，既然有共边定理，是否存在共角定理呢？答案是肯定的！我们先来看一个常见的题目．

例1如图1, P 、 Q 分别在△ ABC 的边 AB 、 AC 上，且 AB =3AP, AC =4AQ求△ APQ 和△ ABC 的面积之比。

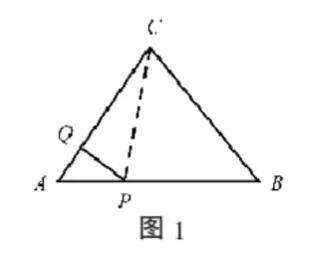
作辅助线，用△APC过渡

解：连接 CP ，则

探究例1的本质，我们发现△ ABC 和△ APQ 有公共角 ∠A ，而题目所牵涉到的“线段”都是在 ∠A 的两边，而不是在 BC 或 PQ 上．例1的解答，则是通过作辅助线，将两个共角的三角形转化为共边的三角形。把这个例子推广到一般的情形，就是共角定理．

共角定理：△ ABC 和△ XYZ 中，若 ∠ABC 和 ∠XYZ 相等或互补，有

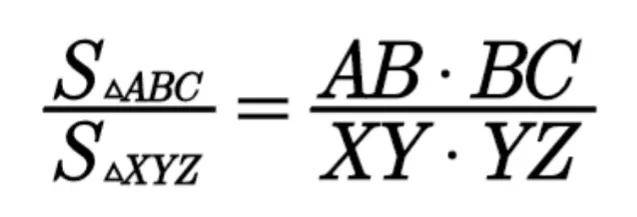
共角比例定理

形象地说，共角定理就是指，两个三角形，若有一个角相等(或互补)，则这两个三角形的面积之比就等于（夹这个角的）各自两边之比.

同角相等

互补角

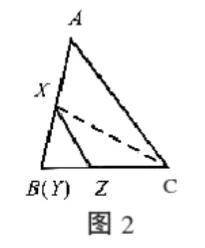
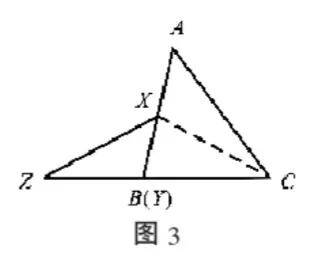
证明：如图2、图3，仿照例1的证明，

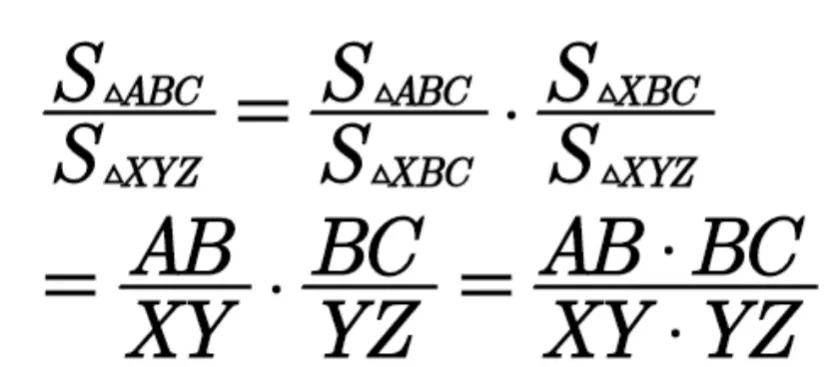
共角定理的证明

我们以前说过，一个定理重要与否，要看它解决问题的多少，也要看它应用范围的大小．一般来说，应用范围较小的命题是不能称之为定理的．下面，我们就来看一看共角定理的威力到底有多大．

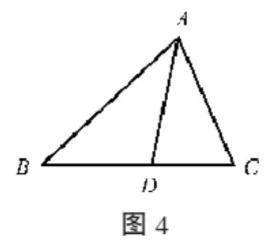
例2（角平分线定理）如图4，在△ ABC 中，已知 AD 是 ∠BAC 的角平分线．求证： AB:AC= BD:DC

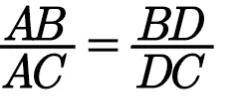
证明：

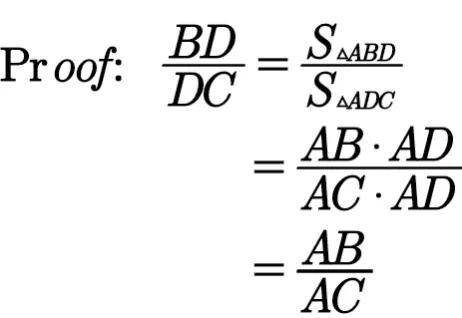
证明角平分线定理

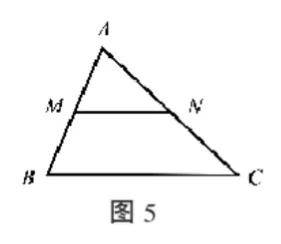
例3（三角形中位线定理）如图5所示，在△ ABC 中， AB 的中点为 M ，过 M 作 BC 的平行线与边 AC 交于 N ．求证：

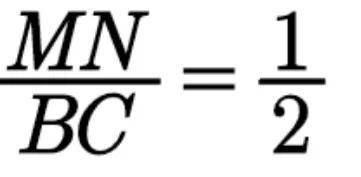
证明：由 MN // BC 可知∠ANM = ∠C ．由共角定理可得

证明三角形中位线定理

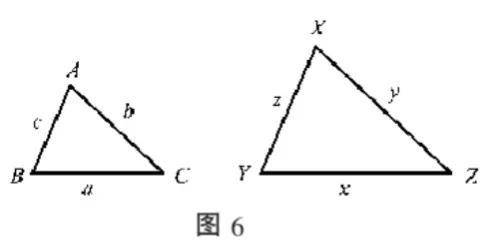
例4 如图6，已知△ ABC 和△ XYZ 中， ∠A = ∠X , ∠B =∠ Y ．求证：

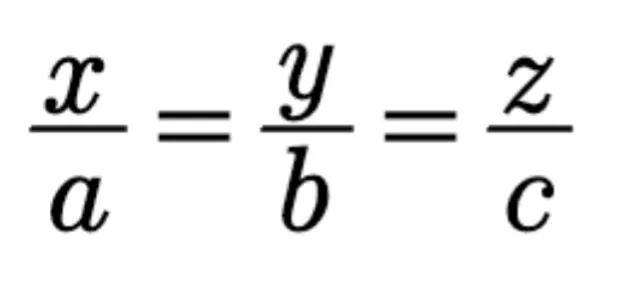
证明：由题意可知 ∠C = ∠Z ，由共角定理可得

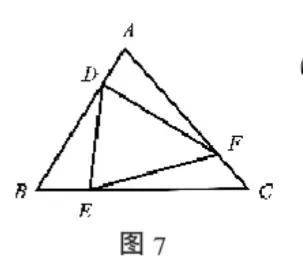
例5 如图7，点 D 、 E 、 F 分别为△ ABC 三边上的点，且

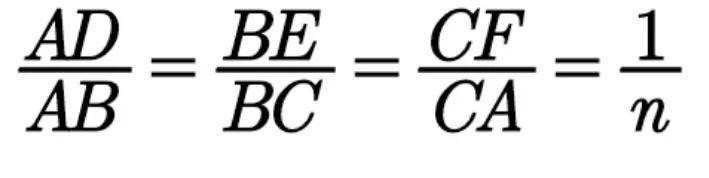
求证：

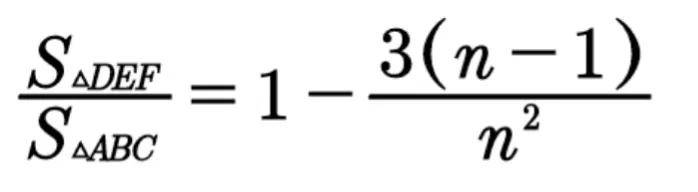
证明：

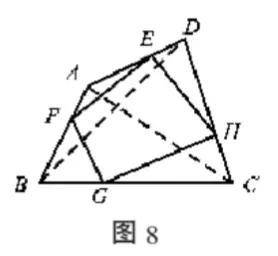
例6 如图8，点E、F、G、H分别为四边形ABCD各边上的点，且

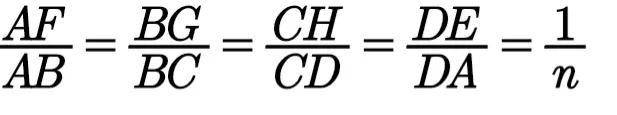
求证：

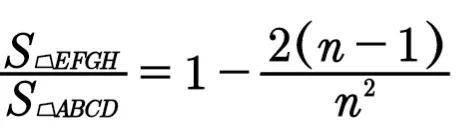
证明：由共角定理，

读后感

看完角平分线定理的例题，想到了库斯顿定理：

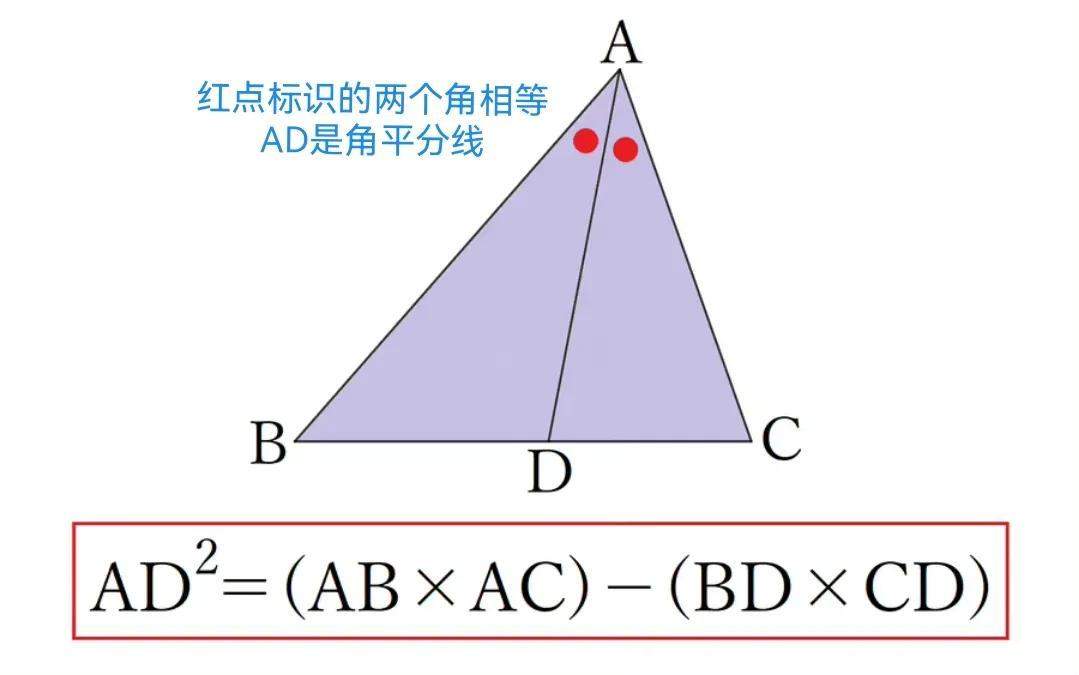
荷兰数学家库斯顿发现的定理

这个定理怎么证明呢？请看我以前的文章：从斯图尔特定理谈起

科学尚未普及，媒体还需努力。感谢阅读，再见。