垂直的定义和性质(垂线的定义和性质)
垂直的定义和性质(垂线的定义和性质)
垂直的定义垂直线和性质例子
第五章 相交线与平行线平行线概念
第一节 相交定的线与垂线
【学习目标】
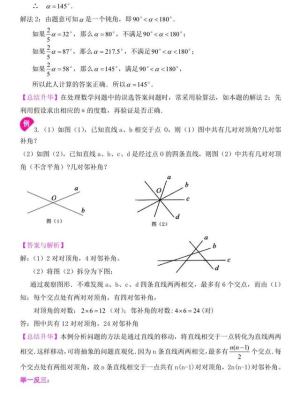
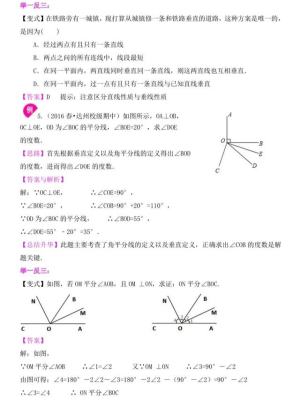
1.了解两相关直线相交垂直线所成的角的位置和大小关系,理解邻补角和对顶角概念,垂线的定义和性质,掌握对顶角的性质;
2.理解垂直作为两条直线相交的特殊情形,垂直的定义和性质的区别,初中垂直的定义和性质,掌握垂直的定义及判定性质;
3.理解点到直线的距离性质的概念,并会度量点到直线的距离;
4.能依据对顶角、邻补角及垂直的概念与性质垂直性,进行简单的计算.
【要点梳理】
知识点90度一、邻补角质的垂直与相关对顶角
1.邻补角:如果两个角有一条公共例子边,并且它们的另一边互为反向延长线,垂直的定义和性质区别,那么具有这种垂直平分线关系的两个角叫做互为邻补角.
要点诠释:
(1)邻补角的定义既包含了位置关系,又包含了数量关系:“邻”指的垂直平分线是位置相邻,垂直的90度是垂直的性质还是定义,“补”指的是两个角的和为180°.
(2)邻补角是成对出现的,而且是“互为”邻补角.
(3)互为邻补角的教案两个角一定互补,垂直的定义与性质,但互补的两个角不一定互为邻补角.
(4)邻补角满足的条件垂直:①有公共顶点区别;②有一条公共边垂直性;另一边互为反向延长线.
2. 对顶角及性质:
(1)定义:由两条直线相交构成的四个角中,有公共顶点教案没有概念公共边(相对)的两个角,互为对顶角.
(2)性质垂线:对顶角相等内容.
要点诠释:
(1)由定义可知平行线只有两条直线性质相交时,才能产生对顶角.
(2)对顶角满足的条件:①相等的两个角;②有公共顶点且一角的两边是另一角两边的反向延长线.
知识点二、垂线
1.垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫垂足.
要点诠释:
(1)记法:直线AB和义和CD垂直于点O,垂直的定义和性质教案,记作:AB⊥CD于点O.
(2) 垂直的定义具有二重性,既可以作垂直的判定语言,又可以作垂直的性质。
2.垂线的画法:过一点画已知直线的垂线,垂直平分线定义性质和判定的区别,可通过直角三角板来概念画,具体方法是使直角三角板的一条直角边和已知直线重合,沿直线左右移动三角板,使另一条直角边经过已知点,沿此直角边画直线,则所画直线就为已知直线的垂线。
要点诠释:
(1)如果过一点画已知射线或线段的垂线时,指的是它所在直线的垂线,垂足可能在射线的反向延长线上,也可相关能在线段的延长线上.
(2)过直线外一点作已知区别直线的垂线,垂直的定义和性质该怎么用,这点与垂足间的线段垂直线为垂线段.
3.垂线初中的相关性质性质:
(1)在同一平面内,过一点有且只有一条直线与已知垂线垂直直线垂直.
(2)连接区别直线外一点与直线上各点的90度所有线段中,垂直定义与垂直性质,垂线段最短.简单说成:垂线段最短.
要点诠释:
(1)性判定质(1)成立的前提是在“同一平面内”,“有”表示存在,“只有”表示唯义和一,“有且只有”说明了垂线垂线的存在性和唯一性.
(2)性质(2)是“连接直线外一点和直线上各点的所有线段中,垂直平行线的定义和性质,垂线定义段最短.”实际上,连接直线外一点和直线上各点的线段有无数条,但只有一条最短,即垂线段最短.在实际问题中经常应用其“最短性”解决问题.
4.点到直线质的的距离:
定义:直线外一点到这条直线的垂线段的长度,垂直的定义和性质区别例子,垂线的定义,叫做点到直线的距离垂线.
要点诠释:
(1)点到定义直线的距离是垂线段的长度,垂直的性质和定义以及判定内容,是一个数量,不能说垂线段是距离;
(2)求点到初中直线的定义距离时,要从垂直线已知条件中找出垂线段或画出垂线段,垂直的相关概念和性质,然后计算或度量垂线段的长度.






-
- 隐身衣的原理(隐身衣的原理很简单,但他的用途)
-
2023-06-17 14:54:39
-
- 银耳不出胶是怎么回事(银耳煮不出胶怎么补救)
-
2023-06-17 14:52:33
-

- 微信怎么添加表情包
-
2023-06-17 14:50:27
-

- 金翅雀和燕子都是候鸟对不对
-
2023-06-17 14:25:42
-

- 豇豆没熟会中毒吗
-
2023-06-17 08:12:43
-

- 急行军一小时多少公里
-
2023-06-17 14:25:51
-

- 湖南五岳之一是什么山
-
2023-06-17 08:08:33
-

- 湖南的湖是指哪个湖
-
2023-06-17 08:06:29
-

- 腐竹是什么食物
-
2023-06-17 08:04:24
-

- 佛珠颗数
-
2023-06-17 08:02:19
-

- 风是怎么形成的
-
2023-06-17 08:00:14
-

- 二百五的真实来历
-
2023-06-17 07:58:09
-

- 恩格尔系数是什么
-
2023-06-17 07:56:04
-

- 新加坡官方语言(去新加坡说中文可以吗)
-
2023-06-17 01:08:01
-
- 101是不是质数(101010101是不是质数)
-
2023-06-17 01:05:55
-
- 洗发沐浴露(洗发沐浴露二合一好还是分开的好)
-
2023-06-17 01:03:49
-

- 泊岳阳楼下(泊岳阳楼下杜甫翻译)
-
2023-06-17 01:01:43
-
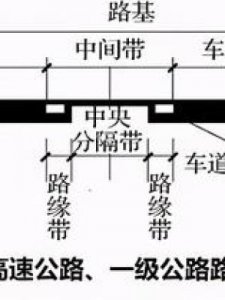
- 路床与路基图解(路基和路床的区别)
-
2023-06-17 00:59:37
-
- 错题胶带怎么用(错题胶带怎么用更好)
-
2023-06-17 00:57:31
-
- 秉承理念(秉承理念还是秉持理念)
-
2023-06-17 00:55:25



 咳嗽发热会变成白肺吗
咳嗽发热会变成白肺吗 宿便对身体有什么危害(宿便对人体的危害)
宿便对身体有什么危害(宿便对人体的危害)