什么是整式,什么是整式。和分式有什么区别?
什么是整式,什么是整式。和分式有什么区别?
什么是整式和分式有什么区别
在整式中除数不能含有字母:2x/3、0.4X 3、x*y是整式。分式是除数中至少有一个字母,x/y是分式。
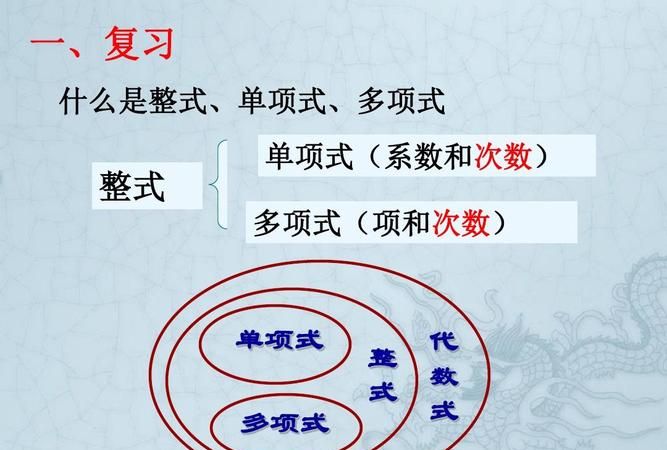
为什么一次函数是整式
要回这问题先了解什么是整式,整式指的是单项式和多项式。单项式又指的是数与字毌的乘积的式子。多项式指的是几个单项式的和的式子。弄清了上面概念后,接下来是一次函数表达式:y=kx+b,k≠0,kx+b是一个多项式,所以一次函数表达式为整式。

什么是整式______,整式中如有分母,分母______(含、不含)字母
试题答案:单项式和多项式统称整式.整式中如有分母,分母不含(含、不含)字母.故答案是:单项式和多项式统称整式;不含.
什么叫整式X+2是单项式还是多项式.整式和代数式的区别是什么
上课找答案啊!整式相对的是分式,都属于代数式,好多年了,应该是这样吧。X+2是两个单式项之和,当然是多项式。
含自变量的代数式是整式是什么意思
含有自变量的代数式是整式的意思是这个代数式是多项式和单项式。理由如下:整式包括单项式和多项式,数与字母的积叫做单项式,单独一个数或一个字母也是单项式,如2xy,4,a等。几个单项式的和叫做多项式,如x-xy.等。要注意的是整式里面不包括分式,字母中含有字母的代数式。
数和整式的区别
数(拼音:shù、shǔ、shuò)“数”本义是查点、统计,引申指列举过错,加以惩罚,如:数落;又引申指比较起来最突出的,如:数一数二;表示以上动词意义时,均读作shǔ。数又读作shù,表示数目的意思,用作名词;又引申指计算、量化的符号,如数码、数字;又引申指不确定的约数,如数次、数年。数又读作:shuò,表示频繁的意思,用作副词。
整式为单项式和多项式的统称,是有理式的一部分,在有理式中可以包含加,减,乘,除、乘方五种运算,但在整式中除数不能含有字母。
整式包括什么和什么
单项式和多项式统称为整式。代数式中的一种有理式.不含除法运算或分数,以及虽有除法运算及分数,但除式或分母中不含变数者,则称为整式。 (含有字母有除法运算的,那么式子 叫做分式fraction.)整式可以分为定义和运算,定义又可以分为单项式和多项式,运算又可以分为加减和乘除。加减包括合并同类项,乘除包括基本运算、法则和公式,基本运算又可以分为幂的运算性质,法则可以分为整式、除法,公式可以分为乘法公式、零指数幂和负整数指数幂。整式和同类项1.单项式(1)单项式的概念:数与字母的乘积这样的代数式叫做单项式,单独一个数或一个字母也是单项式。注意:数与字母之间是乘积关系。(2)单项式的系数:单项式中的 数字因数及性质符号叫做单项式的系数。如果一个单项式,只含有数字因数,是正数的单项式系数为1,是负数的单项式系数为—1。(3)单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。2.多项式(1)多项式的概念:几个单项式的和叫做多项式。在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。一个多项式有几项就叫做几项式。多项式中的符号,看作各项的性质符号。一元N次多项式最多N+1项(2)多项式的次数:多项式中,次数最高的项的次数,就是这个多项式的次数。(3)多项式的排列:1.把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列。2.把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列。由于多项式是几个单项式的和,所以可以用加法的运算定律,来交换各项的位置,而保持原多项式的值不变。为了便于多项式的计算,通常总是把一个多项式,按照一定的顺序,整理成整洁简单的形式,这就是多项式的排列。在做多项式的排列的题时注意:(1)由于单项式的项,包括它前面的性质符号,因此在排列时,仍需把每一项的性质符号看作是这一项的一部分,一起移动。(2)有两个或两个以上字母的多项式,排列时,要注意:a.先确认按照哪个字母的指数来排列。b.确定按这个字母向里排列,还是生里排列。(3)整式:单项式和多项式统称为整式。(4)同类项的概念:所含字母相同,并且相同字母的次数也相同的项叫做同类项,几个常数项也叫同类项。掌握同类项的概念时注意:1.判断几个单项式或项,是否是同类项,就要掌握两个条件:①所含字母相同。②相同字母的次数也相同。2.同类项与系数无关,与字母排列的顺序也无关。3.几个常数项也是同类项。(5)合并同类项:1.合并同类项的概念:把多项式中的同类项合并成一项叫做合并同类项。2.合并同类项的法则:同类项的系数相加,所得结果作为系数,字母与字母的指数不变。整式和整式的乘法整式可以分为定义和运算,定义又可以分为单项式和多项式,运算又可以分为加减和乘除。加减包括合并同类项,乘除包括基本运算、法则和公式,基本运算又可以分为幂的运算性质,法则可以分为整式、除法,公式可以分为乘法公式、零指数幂和负整数指数幂。同底数幂的乘法法则:同底数幂相乘,底数不变指数相加。幂的乘方法则:幂的乘方,底数不变,指数相乘。积的乘方法则:积的乘方等于把积的每一个因式分别乘方,再把所得的幂相乘。单项式与单项式相乘有以下法则:单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。整式是代数式中最基本的式子,引进整式是实际的需要,也是学习后续内容(例如分式、一元二次方程等)的需要。整式是在以前学习了有理数运算、列简单的代数式、一元一次方程及不等式的基础上引进的。事实上,整式的有关内容在六年级已经学习过,但现在的整式内容比过去更加强了应用,增加了实际应用的背景。
-

- 森林防火严戒期是什么时候,森林防火严戒期是什么时候开始
-
2023-09-04 04:52:03
-

- 山羊的脚印像什么花呢,山羊的脚印像什么图案
-
2023-09-04 02:08:35
-
- 热传播途径有哪些,热的传播的三种方式什么时候学的
-
2023-09-04 02:06:27
-

- 期待落空写一段话,期待落空的情景写一段话100字
-
2023-09-04 02:04:21
-

- 烤面筋酱料的秘制配方,家庭烤面筋的酱料怎么调制
-
2023-09-04 02:02:13
-

- 金器怎么清洗,18k金用火烧了变色了怎么清洗?
-
2023-09-04 02:00:07
-

- 红烧啤酒鹅怎么做好吃窍门,鹅肉怎么做好吃家常做法
-
2023-09-04 01:58:01
-

- 2024奥运会在哪个国家,下一庙奥运会在哪一个国家举办?
-
2023-09-04 01:55:54
-
- 最早的航海图集是,世界上现存最早的航海图集是
-
2023-09-04 01:53:47
-

- 怎么刷白鞋干净又不发黄,怎么刷白布鞋干净又不发黄?
-
2023-09-04 01:51:41
-

- 怎么处理魔芋的腥味,魔芋丝有股腥味
-
2023-09-04 01:49:34
-

- 爱粮节粮小妙招,有哪些节约粮食的妙语?
-
2023-09-03 13:40:01
-

- 嫦娥古诗意思,嫦娥古诗分段意思?
-
2023-09-03 13:37:56
-
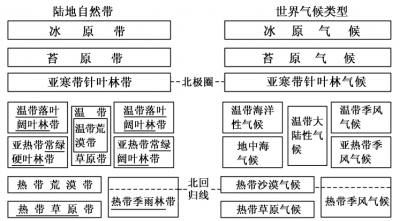
- 从自然条件看,我国地跨几个气候带,从自然条件看我国跨几个气候带?
-
2023-09-03 13:35:51
-

- 地坪漆施工工艺,薄涂地坪漆施工工艺?
-
2023-09-03 13:33:46
-
- 房州是现在的什么地方,明朝黄州府现在是哪里
-
2023-09-03 13:31:41
-

- 佛心果的颜色是天然的还是人工的,佛心果的颜色是怎么染的?
-
2023-09-03 13:29:36
-

- 格林童话有哪些,格林童话和安徒生童话各有哪些?请分别列出,别复制一推废话
-
2023-09-03 13:27:31
-

- 花胶放久了可以吃,花胶放了三年还能吃吗
-
2023-09-03 13:25:26
-

- 欢迎新老师加入欢迎词,家长欢迎新老师进群的欢迎词?
-
2023-09-03 13:23:22



 赵薇在万家文化事件中获利多少(被遗忘的黄有龙)
赵薇在万家文化事件中获利多少(被遗忘的黄有龙) 米脂杀害多名中学生现场(米脂中学生遇袭事件)
米脂杀害多名中学生现场(米脂中学生遇袭事件)